K-Means

K-Means

algorithm

1. taking K random points as centroids.
2. For each point, decide which centroid is closer, which forms clusters
3. Move centroids to the mean of the clusters
4. repeat 2-3 until centroids are not moving anymore

K-Means++

It is smart initialization method. When adding one more point, no optimal is often happen if two points are close. Thus, pick next point with probabilty proportional to distance from the centroid.

$$distance(x_i)^2)/\sum_{j=1}^{K}distance(x_j)^2$$

Choosing right K

e.g.)
K = cpu core
K is fixed to target number of clusters

Intertia

Similar values corresponds to tighter clusters. But Value senstivie to number of points in cluseter

$$\sum_{i=1}^{K}distance(x_i,c_i)^2$$

Distortion

Adding more points will not increase distortion.

$$1/n \sum_{i=1}^{n}distance(x_i,c_i)^2$$

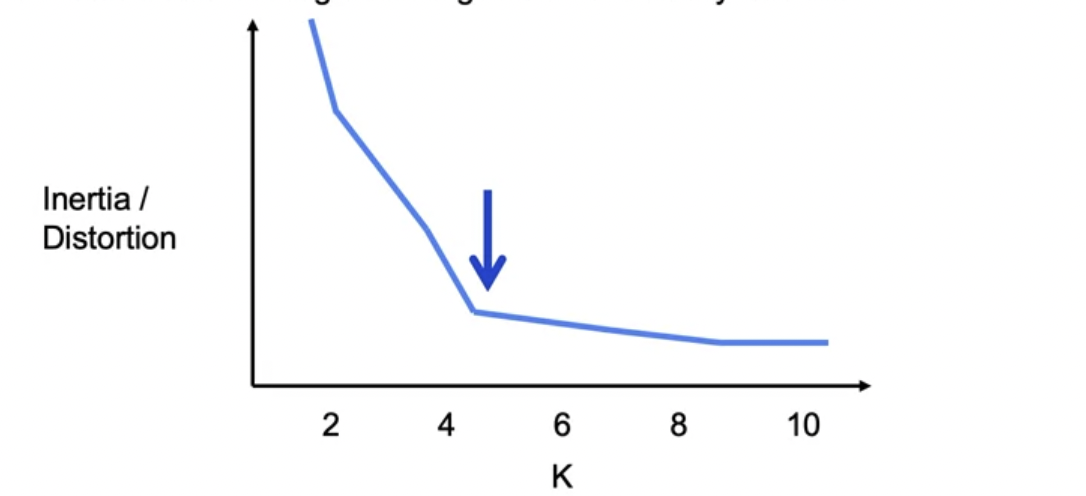
Elbow Method

We initiate K-mean several times, and choose the one with lowest distortion or inertia. Find a point where the decrement of value is lower.

Code

from sklearn.cluster import KMeans, MiniBatchKMeans

kmeans = Kmeans(n_clusters=3, init='k-means++', max_iter=300, n_init=10, random_state=0)
kmeans = kmeans.fit(X1)
y_predict = kmeans.predict(X2)

Inertia

inertia = []
list_clusters = list(range(10))
for k in list_clusters:
    kmeans = KMeans(n_clusters = k)
    kmenas.fit(X1)
    inertia.append(kmeans.inertia_)